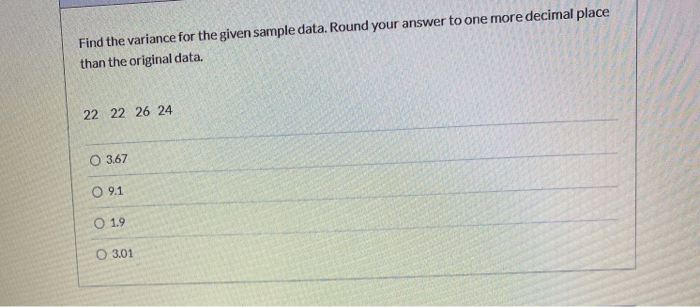
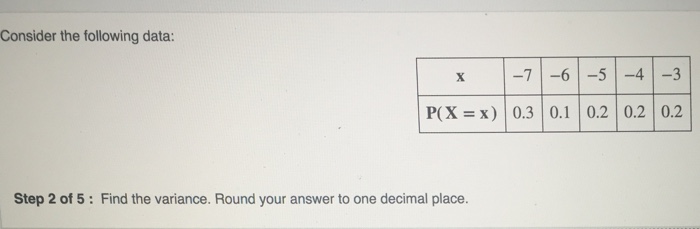
Find the variance. Round your answer to one decimal place. Delving into the intricacies of variance, this comprehensive guide unveils its significance in statistics, exploring its formula, methods of calculation, applications, and implications in hypothesis testing. Prepare to unravel the secrets of variance and harness its power in data analysis.

Variance, a fundamental concept in statistics, quantifies the dispersion or spread of data points around their mean. Understanding variance is crucial for making informed decisions and drawing meaningful conclusions from data.

Variance

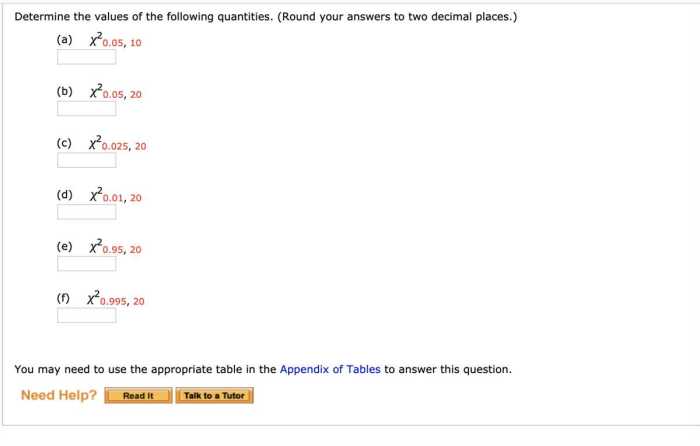
Variance is a statistical measure that quantifies the spread or variability of data points from their mean. It represents the average squared difference between each data point and the mean of the data set.

Definitions and Formulae

The variance of a data set is calculated using the following formula:

σ²= Σ(x

• μ) ²/ (N
• 1)

where:

• σ ²is the variance
• x is each data point
• μ is the mean of the data set
• N is the number of data points

Methods for Calculating Variance

To calculate variance, follow these steps:

1. Calculate the mean of the data set.
2. Subtract the mean from each data point to find the deviations.
3. Square each deviation.
4. Sum the squared deviations.
5. Divide the sum by N
   

   1 to find the variance.

Statistical software or calculators can also be used to calculate variance.

Variance and Standard Deviation

Variance is related to standard deviation, which is the square root of variance:

σ = √σ²

Standard deviation measures the spread of data points in the same units as the original data.

Applications of Variance

Variance has applications in various fields, including:

• Finance: Assessing the risk of investments
• Economics: Measuring economic growth or volatility
• Quality control: Evaluating the consistency of products or processes

Variance in Hypothesis Testing, Find the variance. round your answer to one decimal place.

Variance plays a role in hypothesis testing, where it is used to determine the statistical significance of results.

For example, in a t-test, the variance of the two data sets being compared is used to calculate the t-statistic, which determines whether there is a statistically significant difference between the means of the two sets.

Assumptions and Limitations

The use of variance assumes that the data is normally distributed.

Additionally, variance can be affected by outliers, which are extreme values that may not represent the typical behavior of the data.

Clarifying Questions: Find The Variance. Round Your Answer To One Decimal Place.

What is the formula for calculating variance?

Variance is calculated as the sum of squared deviations from the mean divided by the number of observations minus one (n-1).

How is variance related to standard deviation?

Standard deviation is the square root of variance. It represents the typical distance between data points and the mean.

What are the applications of variance in real-world scenarios?

Variance is used in risk assessment, quality control, financial analysis, and many other fields to evaluate the variability of data.