Embark on a mathematical adventure as we dive into the captivating world of percentages! What percent of 10.5 is 32.76? Hold on tight, because we’re about to uncover the secrets behind this intriguing calculation.
Join us as we unravel the mysteries of percentage, exploring its relationship with fractions and decimals. We’ll guide you through a step-by-step journey, empowering you to conquer any percentage problem that comes your way.
Understanding the Concept of Percentage

Percentage is a way of expressing a fraction as a hundredth. It is represented by the symbol %. For example, 50% means 50 hundredths, which is the same as 0.5 or 1/2.
Relationship Between Percentage, Fraction, and Decimal
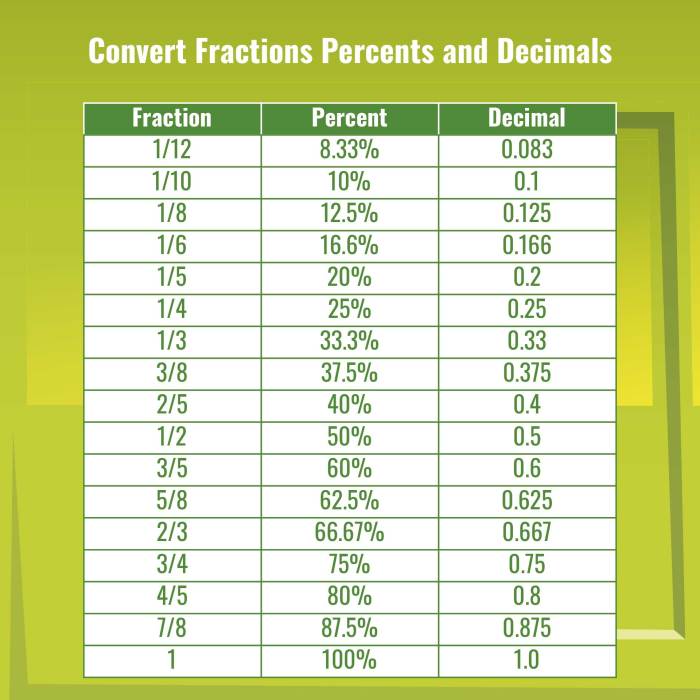
The following table shows the relationship between percentage, fraction, and decimal:
| Percentage | Fraction | Decimal |
|---|---|---|
| 50% | 1/2 | 0.5 |
| 25% | 1/4 | 0.25 |
| 10% | 1/10 | 0.1 |
Calculation of Percentage
Calculating percentages is a fundamental skill that is used in various aspects of our daily lives. Understanding the concept of percentage is essential for making informed decisions and solving mathematical problems. In this section, we will delve into the step-by-step procedure for finding the percentage of a given number.
So, what percent of 10.5 is 32.76? It’s a simple calculation that can be done in your head. But if you’re looking for a more in-depth explanation, check out the amsco book ap human geography . It’s a great resource for students who are studying for the AP Human Geography exam.
And it can help you understand the concept of percentages and how to apply them to real-world problems. So, if you’re struggling with this topic, be sure to check out the amsco book ap human geography.
Step 1: Understand the Concept of Percentage
Percentage is a way of expressing a fraction as a hundredth. The symbol “%” represents percentage. For example, 50% means 50 out of 100, or half of the whole.
Step 2: Convert the Percentage to a Decimal
To calculate the percentage of a number, we first need to convert the percentage to a decimal. To do this, we divide the percentage by 100.
Decimal = Percentage / 100
For example, to convert 50% to a decimal, we divide 50 by 100, which gives us 0.5.
Step 3: Multiply the Decimal by the Number
Once we have converted the percentage to a decimal, we can find the percentage of a number by multiplying the decimal by the number.
Percentage of a Number = Decimal x Number
For example, to find 50% of 100, we multiply 0.5 by 100, which gives us 50.
Example, What percent of 10.5 is 32.76
Let’s say we want to find 25% of 200. Using the steps Artikeld above:
- Convert 25% to a decimal: 25 / 100 = 0.25
- Multiply the decimal by 200: 0.25 x 200 = 50
Therefore, 25% of 200 is 50.
Application of Percentage

Percentages are a ubiquitous concept in our daily lives, finding applications in a wide range of fields. From financial calculations to economic analysis and everyday measurements, percentages provide a convenient and standardized way to express proportions and relationships.
Finance
In finance, percentages play a crucial role in calculations related to interest rates, loans, and investments. Banks use percentages to determine the interest charged on loans and the returns on investments. For example, if you borrow $10,000 at an interest rate of 5%, you will pay $500 in interest each year, which is 5% of the principal amount.
Economics
In economics, percentages are used to measure inflation, unemployment, and economic growth. For instance, if the inflation rate is 2%, it means that the average price of goods and services has increased by 2% over the past year. Similarly, if the unemployment rate is 10%, it indicates that 10% of the workforce is unemployed.
Everyday Life
Percentages are also prevalent in everyday life. We use them to calculate discounts, determine the percentage of alcohol in a drink, and measure the progress of a project. For example, if a store offers a 20% discount on a product, you will pay 20% less than the original price.
Likewise, if a bottle of wine contains 12% alcohol, it means that 12% of the liquid is pure alcohol.
Solving Percentage Problems

Percentage problems involve finding a part of a whole or expressing a value as a percentage of another value. To solve these problems effectively, we can use the formula:
Percentage = (Part / Whole) – 100
Let’s practice applying this formula to solve some percentage problems:
Practice Problems
- Find 25% of 80.
- Express 12 as a percentage of 60.
- A store has a sale where all items are 20% off. If a shirt originally costs $30, what is the sale price?
- A company’s sales increased by 15% last year. If their sales were $1,000,000 the previous year, what were their sales last year?
Advanced Percentage Concepts: What Percent Of 10.5 Is 32.76

In this section, we will explore advanced concepts related to percentage, including the concept of compound percentage and its calculation.
Compound Percentage
Compound percentage refers to the calculation of percentage of a percentage. It involves applying a percentage to a value that is already expressed as a percentage.
The formula for calculating compound percentage is:
Compound Percentage = (Percentage 1
Percentage 2) / 100
Steps involved in calculating compound percentage:
- Convert the percentages to their decimal equivalents by dividing by 100.
- Multiply the decimal equivalents of the percentages.
- Multiply the result by 100 to convert it back to a percentage.
FAQ Compilation
What’s the formula for calculating percentage?
Percentage = (Value / Total Value) x 100
How do I find the percentage of a number?
Follow these steps: 1. Divide the value by the total value. 2. Multiply the result by 100.